For this problem set use the dataset on home characteristics and prices. The data description can also be downloaded.

1. Local government and public schools are largely financed by property taxes. One's property tax bill is based on the tax rate and the assessed value of the house. From time to time the local tax authority must revise the assessed values of houses in the jurisdiction. To bring some regularity to the re-assessment process the authority often uses regression models. The dataset hprice1.wf1 has data on assessed value and house attributes. It is your job to help with the modeling of home attributes and assessed value.

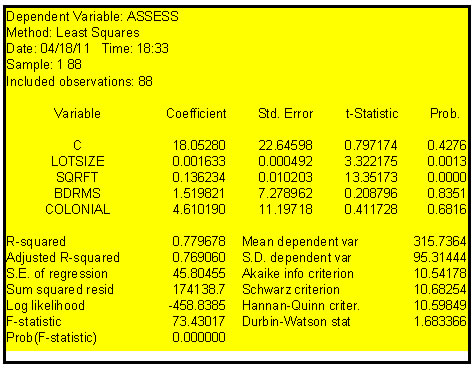
a. Estimate by OLS the regression coefficients of and report your results.

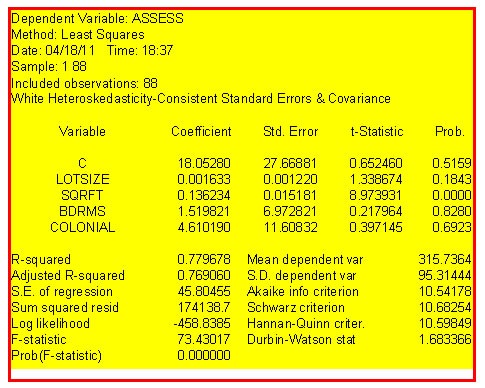
b. For the same model as that in part a, use EVIEWS to find the heteroscedasticity robust standard errors for the coefficients and report your findings.

c.Compare and contrast your results for parts a and b.

The R-sq and the coefficient estimates do not change, but the standard errors of the coefficients do change. Lotsize is not longer signficiant. The other explanatory variables do not show markedly different results.

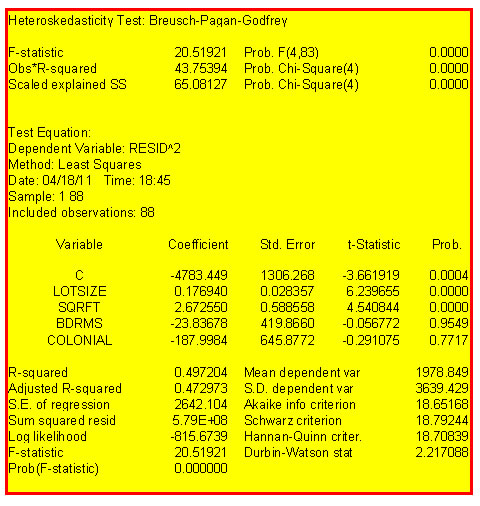
d. Use EVIEWS to conduct a Breusch-Pagan test for heteroscedasticity at the 5% level and report your results.

The null hypothesis is that the model error is homoscedastic. The observed F-statistic is 20.5 and cuts off essentially zero probability in the tail. Therefore, at the 5% level we reject the null.

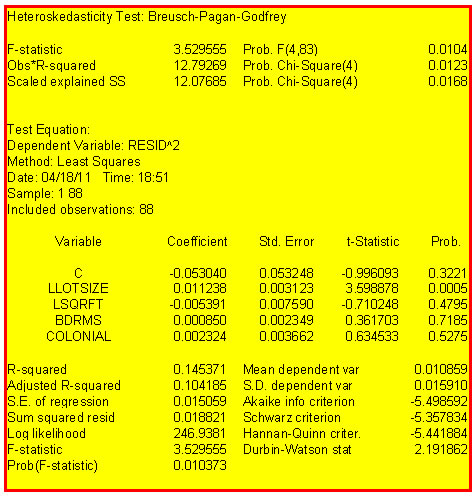
e. Revise the model to by taking logs of assess, lotsize and sqrft, but not bdrms. Conduct a Breusch-Pagan test for heteroscedasticity at the 5% level.

Although the Breusch Pagan statistic is quite a bit smaller, it is still large enough to reject the null hypothesis of homoscedasticity at the 5% level.

f. In reviewing your resutls for aprts d and e, did transforming the data mitigate the heteroscedasticity problem in any way?

Sometimes using log data can reduce the problem of heteroscedasticity. There was some amelioration since we see that the F is much smaller.